ab-test是互联网行业常用的测试方案,这里就不再赘述如何合理的设计ab-test试验方案了,只讨论如何解读ab-test的结果。
案例
某公司进行一次ab-test,试验结果如下,需要对结果进行解读,确定不同方案之间的优劣。

很多不理解ab-test原理的同学会根据转化率数据直接产生错误解读,B方案转化优于A方案。
以下为正确解读
互联网行业,ab-test一般需要采用双样本对照z检验,即检验两个样本对应的总体均值是否有显著性差异(说白了,因为是随机抽取的样本进行测试,样本体现的情况不一定就是全体用户的情况,所以需要做假设检验)。z检验统计量公式为
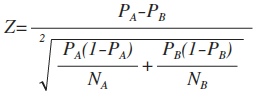
按测试结果将相应的样本数据代入,得到z值为-0.849。说明两个方案没有显著性差异的概率大于5%,这时根据现有测试数据,是无法判定两个方案优劣的。
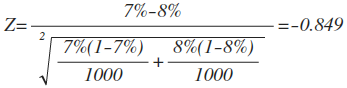
单尾z值与P值的关系

同时根据z值的计算公式,z值与测试的样本量为为正比例关系,即样本量越大,z值越大。因为我们继续拉长测试时间,当两个方案的样本量达到10000时,继续分析测试结果(假定样本量扩大到10000时,转化率仍保持不变)。

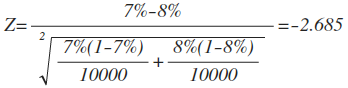
这时重新计算z值,z值等于2.685,这时可以断定A方案和B方案有显著性差异。
样本量确定
有些情况下,在开始设计ab-test实验时,就需要确定需要的样本量大小,便于缩短测试周期,尽快产生测试结论。
那么该如何确定样本量大小呢?
这里只考虑两个方案样本量接近或一致的情况。根据z值的计算公式,可以反推出样本量N的计算公式如下。
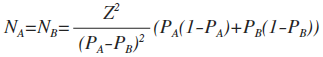
首先要得出可靠结论,z值必须要大于1.96。另外要得出样本量大小,我们还需要知道两个版本的转化率的值,因为没有直接的测试数据,所以采用预估的方式。比如A版本,一般是指原版本,而原版本是有历史数据支持的;B版本是新版本,新版本需要预估转化率能提升多少。
那么,按照A版本7%转化,B版本8%的转化预估。我们需要多少样本才能得出可靠结论。
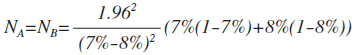
置信区间
部分ab-test工具,会直接提供置信区间,那么置信区间是什么呢?
置信区间是指一个数值范围(m,n)。以上诉案例,表示B版本的转化率与A版本的转化率的差值,落在(m,n)区间内的概率大于95%。当然这个区间对应的是置信水平95%(显著性水平5%)的置信区间。
一般来讲,如果置信区间的上下限同为正,说明试验结果是统计显著的,并且试验版本优于对照版本;如果同为负,试验结果也是统计显著的,且对照版本优于试验版本;如果置信区间为一正一负,则说明版本间差异不大。置信区间的计算公式如下(常数1.96为95%置信水平下的值):
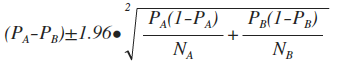
以此计算上述案例中,
样本量为1000时的置信区间为(-3.31%,1.31%),即A版本与B版本转化率差值落在此区间内的概率为95%;
样本量为10000时的置信区间为(-1.73%,-0.27%),即A版本与B版本转化率差值落在此区间内的概率为95%;