我们拿到了某市10000个学生的英语考试得分数据,数据如下。
现在需要了解英语分数的大概情况。我们可以用得分平均值、中位数、众数、方差、标准差等指标来判断得分大概情况,但最直观的方式还是直方图,或者说频率分布图。
首先我们按10为单位,将得分划分为10个组,统计每个组的得分出现的次数及频率

然后根据次数/频率分布表画出直方图
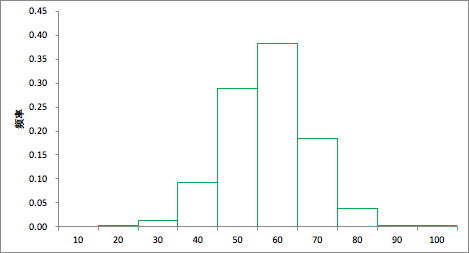
接下来,上图组距为10的直方图,我们可以缩小组距,看看图的变化。下图为组距为5时的直方图
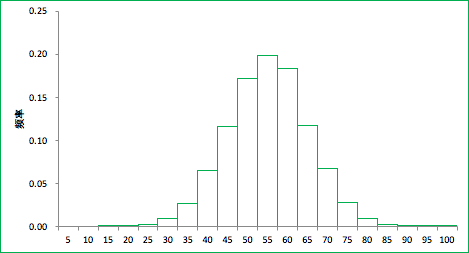
组距为2的直方图
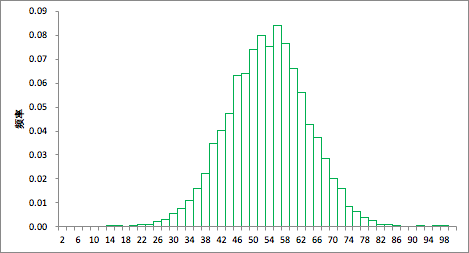
缩小组距的过程中,可以发现直方图越来越接近曲线。直方图中,将组距缩小至极限后,所看到的曲线,即为概率密度函数对应的曲线。理论上概率密度函数是可以有各种形态的,此案例中的形态即为统计学上最常见的正态分布曲线。
正态分布曲线,要记住以下特征:
1、以平均值为中心呈左右对称。
2、受到平均值和标准差的影响,平均值决定了曲线的中心位置,标准差决定了曲线的形态,标准差越小曲线越尖,反之越扁平。
3、平均值为0,标准差为1的正态分布成为标准正态分布。
所有的正态分布,经过标准化后,就是标准正态分布。而通过标准正态分布表,可以求出所有的取值范围概率。